Aspectos gerais dos Direitos e Garantias Fundamentais
Os direitos fundamentais de 1ª dimensão são aqueles que representam o transcurso do Estado Absolutista para o Estado de Direito ou Estado da Legalidade, em que todos são iguais perante a lei e assegura-se a liberdade para todos os indivíduos.
Link para Constituição Federal
Não transcrevemos o dispositivo completo aqui para não ficar entediada a leitura. Porém, ela é extremamente importante e remetemos o aluno para o link a seguir em que há o texto compilado e atualizado da CF/88.
Constituição Federal
Exerça sua Cidadania
Você sabia que pode sugerir uma nova lei ou opinar sobre os projetos de lei em andamento no Senado Federal?
Clique na imagem abaixo e exercite sua cidadania.
Clique na imagem abaixo e exercite sua cidadania.
Sua participação pode mudar a direção da história do Brasil.
RECRUTAS DE 1964 A 1988
Decisão da Justiça Federal de Santa Catarina: serviço militar não
gera direito à indenização de anistiado político
FONTE: Justiça Federal de Santa Catarina
Joaçaba: serviço militar não gera direito à indenização de anistiado político
A Justiça Federal julgou improcedentes oito ações propostas por homens que
prestaram serviço militar obrigatório durante diversos períodos, entre 1946 e 1978, e
pretendiam obter indenização em função da alegada condição de anistiado político.
A juíza Ana Cristina Monteiro de Andrade Silva, da Vara Federal de Joaçaba,
entendeu que haver servido às Forças Armadas, mas sem comprovação de danos,
não confere direito à reparação prevista na Lei 10.559, de novembro de 2002.
Segundo a juíza, a lei estabelece que são considerados anistiados políticos os
militares que, entre 18 de setembro de 1946 e 5 de outubro de 1988 e por motivação
exclusivamente política, tenham sido atingidos por atos revolucionários, sendo
cassados, reformados ou preteridos no exercício de suas funções. “O fato de a
prestação do serviço ter se dado durante o regime de exceção ou no período de
turbulência institucional que se seguiu à Constituição de 1946 não guinda a parte
autora à condição de anistiado político”, concluiu Ana Cristina.
A magistrada observou ainda que, conforme sustentado pela defesa da União, os
autores não apresentaram provas de que tenham sofridos danos físicos ou mentais
por causa de tratamento degradante ou incompatível. Os argumentos se referem
genericamente aos “efeitos do medo por estar separado da família, submetido ao
manuseio de armas de fogo, a privações de toda espécie e a atos de exceção”. As
sentenças foram publicadas na Internet na última terça-feira (20/5/2008), cabendo
recurso ao Tribunal Regional Federal da 4ª Região.
Outra especulação é a despeito das diferenças sálarias decorrentes dos soldos, que ainda tem gente acreditando que é possível tal diferença de 81%. Carissimos, isso é informação "truncada", ou alguém querendo tirar dinheiro seu. Na verdade a lei . 7723/89, 7923/89 e Lei 8.162/91, que previa o possivel pleito indenizatório das diferenças, que informa-se não chega a tamanha porcentagem, e ainda a lei que previa as diferenças para os SERVIDORES MILITARES, COM REAJUSTE DE 28,86%. LEIS 8.622/93 E 8.627/93, já prescreveu para os novos interessados, pois deveriam ter entrado anteriormente, não agora em 2008 ou meados de 2009. Esse é o entendimento do STJ em sua súmula n. 85 que enuncia a prescrição quinquenal (ou seja, cinco anos), para pleito contra União. As diferenças percebidas FORAM DECORRENTES dos interessados que ingressaram com MANDADO DE SEGURANÇA e AÇÃO ORDINÁRIA na época dos fatos, isto é, dentro do lapso temporal dos cinco anos previsto na Súmula do STJ.
Agora para dar uma ajuda, as únicas indenizações pertinentes para 2009 é até que se prove o contrário, são:
Aos militares da reserva das Forças Armadas:
Ações visando o reconhecimento da reforma por incapacidade física definitiva;
• Ações visando à isenção do Imposto de Renda;
• Ações visando o reconhecimento a Melhoria de Reforma por incapacidade física definitiva;
• Ações visando o reconhecimento o direito ao Auxílio Invalidez;
• Ações de cobrança dos descontos indevidos a título de FUSEX, FUSMA e FUNSA (acima de 3% até Março/2001 e de 3,5% a partir de Abril/2001 até os dias atuais);
• Ações de reparação de danos estéticos e físicos decorrente de atividades militares;
• Ações de reparação de danos morais por danos à imagem, honra e da pessoa humana)
Às pensionistas das Forças Armadas:
• Ações visando o reconhecimento a Melhoria de Reforma por incapacidade física definitiva;
• Ações de cobrança dos descontos indevidos a título de FUSEX, FUSMA e FUNSA (acima de 1,5% até Março/2001 e de 3,5% a partir de Abril/2001 até os dias atuais);
Aos militares temporários das Forças Armadas:
• Ações de reintegração ao serviço ativo de militares temporários excluídos, embora portando incapacidade física definitiva;
• Ações de reparação de danos estéticos e físicos decorrente de atividades militares;
• Ações de reparação de danos morais por danos à imagem, honra e da pessoa humana;
Aos Ex-combatentes e seus dependentes:
• Ações visando o reconhecimento de Ex-combatente que realizou vigilância e segurança no litoral brasileiro (Lei 5.315/67 e Lei 8.059/90);
• Ações visando a reversão da pensão de Ex-combatentes às filhas de qualquer idade e situação civil. (Leis 3.765/60 e 4.242/67);
• Ações de Isenção de Imposto de Renda da Pensão de Ex-combatente;
• Ações visando a Assistência Médica e Gratuita;
gera direito à indenização de anistiado político
FONTE: Justiça Federal de Santa Catarina
Joaçaba: serviço militar não gera direito à indenização de anistiado político
A Justiça Federal julgou improcedentes oito ações propostas por homens que
prestaram serviço militar obrigatório durante diversos períodos, entre 1946 e 1978, e
pretendiam obter indenização em função da alegada condição de anistiado político.
A juíza Ana Cristina Monteiro de Andrade Silva, da Vara Federal de Joaçaba,
entendeu que haver servido às Forças Armadas, mas sem comprovação de danos,
não confere direito à reparação prevista na Lei 10.559, de novembro de 2002.
Segundo a juíza, a lei estabelece que são considerados anistiados políticos os
militares que, entre 18 de setembro de 1946 e 5 de outubro de 1988 e por motivação
exclusivamente política, tenham sido atingidos por atos revolucionários, sendo
cassados, reformados ou preteridos no exercício de suas funções. “O fato de a
prestação do serviço ter se dado durante o regime de exceção ou no período de
turbulência institucional que se seguiu à Constituição de 1946 não guinda a parte
autora à condição de anistiado político”, concluiu Ana Cristina.
A magistrada observou ainda que, conforme sustentado pela defesa da União, os
autores não apresentaram provas de que tenham sofridos danos físicos ou mentais
por causa de tratamento degradante ou incompatível. Os argumentos se referem
genericamente aos “efeitos do medo por estar separado da família, submetido ao
manuseio de armas de fogo, a privações de toda espécie e a atos de exceção”. As
sentenças foram publicadas na Internet na última terça-feira (20/5/2008), cabendo
recurso ao Tribunal Regional Federal da 4ª Região.
Outra especulação é a despeito das diferenças sálarias decorrentes dos soldos, que ainda tem gente acreditando que é possível tal diferença de 81%. Carissimos, isso é informação "truncada", ou alguém querendo tirar dinheiro seu. Na verdade a lei . 7723/89, 7923/89 e Lei 8.162/91, que previa o possivel pleito indenizatório das diferenças, que informa-se não chega a tamanha porcentagem, e ainda a lei que previa as diferenças para os SERVIDORES MILITARES, COM REAJUSTE DE 28,86%. LEIS 8.622/93 E 8.627/93, já prescreveu para os novos interessados, pois deveriam ter entrado anteriormente, não agora em 2008 ou meados de 2009. Esse é o entendimento do STJ em sua súmula n. 85 que enuncia a prescrição quinquenal (ou seja, cinco anos), para pleito contra União. As diferenças percebidas FORAM DECORRENTES dos interessados que ingressaram com MANDADO DE SEGURANÇA e AÇÃO ORDINÁRIA na época dos fatos, isto é, dentro do lapso temporal dos cinco anos previsto na Súmula do STJ.
Agora para dar uma ajuda, as únicas indenizações pertinentes para 2009 é até que se prove o contrário, são:
Aos militares da reserva das Forças Armadas:
Ações visando o reconhecimento da reforma por incapacidade física definitiva;
• Ações visando à isenção do Imposto de Renda;
• Ações visando o reconhecimento a Melhoria de Reforma por incapacidade física definitiva;
• Ações visando o reconhecimento o direito ao Auxílio Invalidez;
• Ações de cobrança dos descontos indevidos a título de FUSEX, FUSMA e FUNSA (acima de 3% até Março/2001 e de 3,5% a partir de Abril/2001 até os dias atuais);
• Ações de reparação de danos estéticos e físicos decorrente de atividades militares;
• Ações de reparação de danos morais por danos à imagem, honra e da pessoa humana)
Às pensionistas das Forças Armadas:
• Ações visando o reconhecimento a Melhoria de Reforma por incapacidade física definitiva;
• Ações de cobrança dos descontos indevidos a título de FUSEX, FUSMA e FUNSA (acima de 1,5% até Março/2001 e de 3,5% a partir de Abril/2001 até os dias atuais);
Aos militares temporários das Forças Armadas:
• Ações de reintegração ao serviço ativo de militares temporários excluídos, embora portando incapacidade física definitiva;
• Ações de reparação de danos estéticos e físicos decorrente de atividades militares;
• Ações de reparação de danos morais por danos à imagem, honra e da pessoa humana;
Aos Ex-combatentes e seus dependentes:
• Ações visando o reconhecimento de Ex-combatente que realizou vigilância e segurança no litoral brasileiro (Lei 5.315/67 e Lei 8.059/90);
• Ações visando a reversão da pensão de Ex-combatentes às filhas de qualquer idade e situação civil. (Leis 3.765/60 e 4.242/67);
• Ações de Isenção de Imposto de Renda da Pensão de Ex-combatente;
• Ações visando a Assistência Médica e Gratuita;
“Desigrejados” no pais já faz um “reboliço santo” no meio da igreja institucional
Irmão Rubens, o desigrejado mais popular da Web!!!
Desigrejados e decepcionados com a igreja
Desigrejados e decepcionados com a igreja
Um fenômeno espiritual que surgiu em nossos dias denominado de os desigrejados da igreja evangélica
Quando uma pessoa passa a frequentar uma igreja, ela cria uma expectativa. Todos nós, que não nascemos em berço evangélico, passamos por isso e sabemos disso. Esperamos que na igreja a pessoa seja diferente. Vemos no pastor a figura do representante de Deus. E esperamos do irmão e dos líderes nada menos do que o melhor. Um comportamento exemplar. Amor transbordante. Só que o tempo passa e a gente descobre que membros e líderes de igreja são seres humanos absolutamente normais: erram, pecam, desiludem, às vezes até maltratam
No caso das pessoas que protestam contra os escândalos causados por líderes inescrupulosos, o reverendo ponderou que a situação termina com dois erros de partes distintas: o primeiro, da instituição religiosa, que se torna um fim em si mesma; e um segundo, dos que se afastam, e terminam por deixar de observar alguns mandamentos bíblicos.
A cada dia que passa o povo cristão e evangélico, vão tomando consciência que a sua salvação não dependendo de “Pontes” para alcançar o outro lado do rio da vida. E vão fugindo do sistema templista ora imposto muita das vezes pela igreja, a qual tem como objetivo lhes manter encarcerados em suas ideologias denominacionais e construir os seus reinos terrenos de sobrevivências na terra.
CONCEITO MAIS COMUM DOS “DESIGREJADOS™
“DESIGREJADOS™ é se desvincular dos lugares apelidados de 'igrejas', é seguir a CRISTO e não depender da igreja institucional, das instituições religiosas com placa de igrejas ou igrejolas ou igrejas evangélicas e católica, é sair para fora do sistema religioso, negando o cristianismo - "Sai dela, povo meu, para que não sejas participante dos seus pecados, e para que não incorras nas suas pragas".
A Bíblia fala-nos da unidade da fé (Ef 4.1-16), e isso a igreja orgânica não tem! Seguir ao Senhor Jesus presume-se em pertencer ao Seu rebanho. Conquanto tenhamos pastores (Ef 4.11; Hb 13.7; Jr 3.15), Ele é o Sumo Pastor (1Pd 5.4), “o grande Pastor das ovelhas” e “bispo das nossas almas” (Hb 13.20; 1Pd 2.25).
Aprenda, querido irmão, querida irmã: onde houver gente você se decepcionará. O modelo é só a casca. Para não se frustrar com o ser humano, a única alternativa é fugir do convívio e se trancar num mosteiro ou numa caverna. Mas cuidado. Lembre-se que, ao fazer isso, você estará carregando junto consigo… você mesmo. E você tem um gigantesco potencial de decepcionar a si mesmo, de frustrar a si mesmo, de magoar a si mesmo, de ferir a si mesmo. Imagine então o potencial que você tem de machucar o próximo. E cogite a possibilidade de que o problema não esteja no templo, nos pastores, nos irmãos, no modelo de igreja: esteja em seu próprio coração pecador. Sim, querido, querida: você pode ser o problema. E peço a Deus que você consiga conviver com a pessoa decepcionante, frustrante e magoadora que você é.
Nunca crie expectativas altas demais, porque se o resultado for mediano, você vai se decepcionar.
Nunca crie expectativas altas demais, porque se o resultado for mediano, você vai se decepcionar.
Já se sua expectativa for baixa e o resultado for mediano, você ficará feliz”. A lição de minha mãe nada mais é do que um mecanismo para evitar a decepção. O desapontamento. A frustração. E o maior deles seria não esperar demais de nada nem de ninguém. Eu acreditei nisso por muitos anos. Mas hoje vejo que ela estava errada
Já se sua expectativa for baixa e o resultado for mediano, você ficará feliz”. A lição de minha mãe nada mais é do que um mecanismo para evitar a decepção. O desapontamento. A frustração. E o maior deles seria não esperar demais de nada nem de ninguém. Eu acreditei nisso por muitos anos. Mas hoje vejo que ela estava errada
Campus Porto Velho Zona Norte disponibiliza livros didáticos on-line
Publicado: Quinta, 02 de Março de 2017, 18h45 | Última atualização em Quinta, 02 de Março de 2017, 18h50 | Acessos: 563
O Instituto Federal de Educação, Ciência e Tecnologia de Rondônia (IFRO), Campus Porto Velho Zona Norte, através do Departamento de Produção de Educação a Distância (DEPEaD), disponibilizou na internet, o material didático produzido para os cursos da EaD. São livros nas áreas de Educação, Informática e Finanças e o objetivo da ação é garantir aos estudantes e professores o acesso ao material.
O acervo foi disponibilizado em um site de livros digitais que possibilita maior interatividade nos processos de leitura. As obras podem ser acessadas em computadores, tablets e smartphones.
“Podemos dizer que o projeto é uma biblioteca de bolso, porque os estudantes têm acesso aos materiais didáticos de forma interativa e portátil, além de ampliar as possibilidades de leitura, pesquisa e estudos, tanto de estudantes da EaD do IFRO quanto de parceiros”, comentou a professora Ariadne Joseane Felix, coordenadora do Departamento de Educação a Distância.
Para conhecer o acervo digital, acesse o link: https://goo.gl/O82L0T.
Convenção e conversão de taxas
Algumas das taxas de juro utilizadas no mercado são definidas como ‘taxa de juro nominal’, como no caso do juro da poupança. Mas o que significa isso? Uma taxa nominal não é a que ganhamos, ou pagamos, efetivamente no fim do período, de um ano, por exemplo. Neste caso precisamos calcular, a partir da taxa nominal, a taxa efetiva embutida na operação. Ou seja, são muitas as convenções adotadas no mercado no que se refere a taxa de juros, e precisamos entender cada uma delas, do contrário não saberemos quanto pagamos por um empréstimo ou quanto recebemos por uma aplicação, além de nos impedir de converter essa taxa para períodos distintos.
.
TAXA NOMINAL E TAXA EFETIVA
Chama-se de taxa efetiva a taxa de juros que se obtém no processo de formação dos juros em regime composto, isto é, ao longo dos períodos de capitalização (geralmente ao longo dos meses). Quando é chamada de taxa nominal estamos tratando de uma definição matemática que considera que o intervalo de capitalização desse juro não é o mesmo daquele definido para a própria taxa. Por exemplo, suponhamos uma taxa nominal de juros de 12% ao ano. Caso não se diga mais nada esta taxa é considerada efetiva, ou seja, a taxa de juros é de 12% ao ano, capitalizada anualmente.
Mas, caso a taxa de juros venha acrescida de um período de capitalização diferente, como ‘12% ao ano, capitalizada mensalmente’, vemos que os prazos não coincidem. Ou seja, o juro de 12% ao ano será capitalizado, incorporado ao principal, no fim de cada mês. Por isso a taxa é chamada de nominal. Neste caso, o prazo de capitalização (ou seja, período de formação e incorporação dos juros ao principal) é de um mês, e o prazo a que se refere a taxa de juros igual é de 1 ano (12 meses). O exemplo mais prático é o caso da poupança, definida em 6% de juro nominal ao ano. Todavia, como somos remunerados mensalmente na caderneta temos que dividir os 6% por 12 meses, o que nos dá 0,5% ao mês. Como temos juros sobre juros, isto é, todo mês a poupança rende 0,5% sobre o que já havia rendido no mês anterior, a taxa efetiva, no fim de 1 ano, acaba sendo de 6,168%; portanto, superior àqueles 6% da taxa nominal divulgada. Logo, temos as seguintes definições a partir deste exemplo da poupança:
.
* taxa nominal da operação para o período = 6% ao ano* taxa proporcional simples (taxa definida para o período de capitalização) = 0,5% ao mês (6%/12 meses)
* taxa efetiva de juros anual (em juro composto) = 6,168% ao ano
CONVERSÃO DE TAXAS: TAXAS PROPORCIONAIS E EQUIVALENTES
Surge um problema ao se converter taxas para períodos distintos. Taxas proporcionais são calculadas em juro simples, precisando neste caso apenas de uma regra de três. Porém, quando falamos em conversão de taxas, geralmente estamos tratando de taxas equivalentes, isto é, em juro composto. Logo,
.
TAXAS PROPORCIONAIS
Qual a taxa mensal proporcional (juros simples) a uma taxa de 6% ao trimestre?
Por regra de três achamos a taxa mensal
6% ____ 3 meses (= 1 trimestre)
x ? ____ 1 mês
x = 2% ao mês
TAXAS EQUIVALENTES
Com o nosso interesse maior aqui é o juro composto, temos a seguinte fórmula para conversão de taxas equivalentes (a juros compostos):

onde,
in = taxa que procuramos
ix = taxa dada
n = dias (ou meses) contidos na taxa procurada
x = dias (ou meses) contidos na taxa dada
Exemplos
1) Qual a taxa mensal proporcional (juros simples) a uma taxa de 6% ao trimestre?
in = mensal (1 mês ou 30 dias)
i = trimestre (3 meses ou 90 dias)
n = 1 meses (ou 30 dias)
x = 1 trimestre (ou 90 dias)
Podemos resolver essa conversão trabalhando com dias ou meses, desde que mantenhamos a compatibilidade ao lançarmos isso na fórmula (mês com mês ou dias com dias).
i30 (dias) = [(1 + 0,06)30/90 (dias) –1] x 100
i30 = [(1,06) 0,3333 –1] x 100
i30 = 1,961%
Ou
i1(mês)= [(1 + 0,35)1/3 (meses) –1] x 100
i1 = [(1,06) 0,3333 –1] x 100
i1 = 1,961%
(f) (REG) 1,06 (ENTER) 30 (ENTER) 90 (÷) (Yx) 1 (-) 100 (x)
i = 1,961%
(f) (REG) 1,06 (ENTER) 1 (ENTER) 3 (÷) (Yx) 1 (-) 100 (x)
i = 1,961%
2) Qual a taxa bimestral equivalente à taxa semestral de 35%?
in = bimestral
i = semestral
n = 60
x = 180
i60 = [(1 + 0,35)60/180 –1] x 100
i60 = [(1,35) 0,3333 –1] x 100
i60 = 10,52%
(f) (REG) 1,35 (ENTER) 60 (ENTER) 180 (÷) (Yx) 1 (-) 100 (x)
i = 10,52%
3) Qual a taxa semestral equivalente à taxa trimestral de 5%?
i180 = [(1 + 0,05)180/90 –1] x 100
i180 = [(1,05) 2 –1] x 100
i180 = 10,25%
(f) (REG) 1,05 (ENTER) 180 (ENTER) 90 (÷) (Yx) 1 (-) 100 (x)
i = 10,25%
4) Qual a taxa diária equivalente à taxa trimestral de 90%?
i1 = [(1 + 0,90)1/90 –1] x 100
i180 = [(1,90) 0,0111 –1] x 100
i180 = 0,7157%
(f) (REG) 1,90 (ENTER) 1 (ENTER) 90 (÷) (Yx) 1 (-) 100 (x)
i = 0,7157%
TAXA NOMINAL (APARENTE) E TAXA REAL
Inflação acumulada
Já vimos em outra lição como considerar o efeito da taxa de inflação ao longo do tempo. Inflação acumulada, que não pode se resumir à soma das inflações. Aprofundemos um pouco esse estudo.
A inflação se processa de maneira exponencial, sendo acrescida sobre a inflação do período anterior, ou seja, o aumento de preço ocorre sobre um valor que já incorpora acréscimos apurados anteriormente. Como nos juros compostos, temos inflação sobre inflação.
Suponhamos que um bem no valor de $ 1.000,00 seja reajustado mensalmente pela inflação, sendo ela de 2,8%, 1,4% e 3,0%, em períodos consecutivos.
1º mês: $ 1.000,00 x (1.028)1 = $ 1.028,00
2º mês: $ 1.028,00 x (1,014)1 = $ 1.042,39
3º mês: $ 1.042,39 x (1,03)1 = $ 1.073,66
O incremento do valor do ativo no trimestre é de 7,366% ($ 1.073,66,/ $ 1.000,00), o que equivale ao produto (capitalização composta) das taxas mensais de inflação, isto é:
.
Inflação do Trimestre = [[(1,028) x (1,014) x (1,03)] –1] x 100 = 7,366%.
* as taxas, quando multiplicadas, dever ser somadas a 1 (link para cálculo da inflação acumulada, por diversos índices, a partir de 2000: http://fundos.economia.uol.com.br/uol/calculadora-indices-inflacao/)
.
A taxa equivalente mensal de inflação do período, identicamente ao regime de juros compostos, é:
Taxa Equivalente Mensal = [(1 + 0,0737)1/3 – 1] x 100 = 2,398% ao mês
* observem que essa taxa equivalente mensal de 2,398% é como uma média das inflações dos 3 meses (2,8%, 1,4% e 3%), pois os resultados são praticamente idênticos, já que (2,8 + 1,4 + 3)/3 = 2,4%. Por isso chamamos a taxa equivalente de taxa média.
.
Se o trimestre apresentasse uma deflação no terceiro mês teríamos: 2,8%, 1,4% e - 3% (deflação). A taxa de inflação acumulada do período seria:Inflação do Trimestre = [[(1 + 0,028) x (1 + 0,014) x (1 – 0,03)] –1] x 100 = 1,11%
Exemplos
1) A taxa mensal de inflação de um quadrimestre (4 meses) atinge, respectivamente: 2,8%, 3,4%, 5,7% e 8,8%. Determinar a taxa de inflação acumulada do período e a taxa média mensal.
(f) (REG) 1,028 (ENTER) 1,034 (x) 1,057 (x) 1,088 (x)
I = 22,2% ao quadrimestre
(f) (REG) 1,222 (ENTER) 4 (1/x) (Yx) 1 (-) 100 (x)
I= 5,15% ao mês
2) A taxa de inflação da economia de determinado ano foi de 748.95%. Calcular a taxa equivalente semestral inflação do período.
(f) (REG) 1 (ENTER) 7,4895 (+) 2 (1/x) (Yx) 1 (-) 100 (x)
I = 191,4% ao semestre
3) Sendo projetada em 1,9% ao mês a taxa de inflação para os próximos 5 meses, determinar a inflação acumulada deste período.
(f) (REG) l,0l9 (ENTER) 5 (Yx) 1 (-) 100 (x)
I = 9,87% p/ 5 meses
4) Determinado trimestre apresenta as seguintes taxas mensais de variações nos preços gerais da economia: 7,2%, 2,9% e - 1,2% (deflação). Determinar a taxa de inflação acumulada do trimestre.
Como temos uma taxa negativa lembremos que:
[(1 + 0,072) x (1 + 0,029) x (1- 0,012)] - 1 = 8,99% a.t.
(f) (REG) 1,072 (ENTER) 1,029 (x) 0,988 (x) 1 (-) 100 (x)
I = 8,99% a.t.
Taxa aparente e taxa real
Já vimos acima que a taxa de juros nominal (linear) indica a descapitalização do juro de forma proporcional (juros simples). No caso da poupança a taxa nominal é de 6%. Todavia o conceito de taxa de juro nominal também pode ter outro significado, neste caso quando a comparamos com a inflação, podendo ser chamada de nominal ou aparente. Lá mostramos a diferença entre taxa nominal e taxa efetiva, pois interessava o regime de capitalização dessa taxa nominal para descobrirmos a efetiva. Como aqui o que importa é o efeito da inflação, separamos a taxa nominal (ou aparente) da inflação e encontramos a taxa real.
O termo real para as operações de Matemática Financeira denota um resultado apurado livre dos efeitos inflacionários. Ou seja, quanto se ganhou (ou perdeu) verdadeiramente, sem a interferência das variações verificadas nos preços. O objetivo do cálculo da taxa real (r) é o de expurgar a indexação da taxa total de juros (nominal), de maneira a expressar o juro real.
A fórmula de apuração da taxa real é a seguinte:
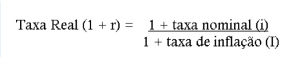
Logo,
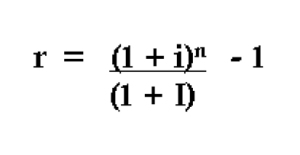
onde:
i = rentabilidade nominal (ou aparente)
I = inflação
r = rentabilidade real
Substituindo-se os valores da inflação e ganho nominal (taxa nominal) do exemplo acima tem-se:
r = [(1 + 0,10) / (1 + 0,20)] - 1 = 1,10 -1 = - 8,33% ($1.000/$12.000)
* A taxa real também pode ser negativa, desde que a inflação supere a variação nominal dos juros.
Comprovação da fórmula:
A inflação tende a corroer o poder de compra da moeda. Suponhamos que uma pessoa tenha adquirido um imóvel por $ 10.000,00 em certa data, e vendido, um ano depois, por $11.000,00. Consideremos ainda uma inflação de 20% no período. É comum diminuir o preço de venda do preço de compra para se determinar o ganho, que neste caso é apenas nominal (ou aparente). Para saber o ganho real, temos que retirar o efeito da inflação no período.
No exemplo, tem-se um lucro nominal (aparente) de $1.000. Observe que para não ocorrer prejuízo, o imóvel deveria ser vendido por um preço 20% maior que o seu valor de compra há um ano, ou seja, por $12.000 (10.000 + 20% de inflação). Somente a partir desse valor é que efetivamente existiria um lucro real. Portanto, a venda por $11.000 mostra um prejuízo real de $1.000,00, pois caso retiremos o preço de venda (11.000) do preço corrigido ($12.000), percebemos o rendimento perdeu para a inflação.
Em termos de rentabilidade notamos que o ganho nominal, como já visto, seria:
Ganho Nominal = $1.000,00/$10.000 x 100 = 10%
Quando consideramos a inflação temos a seguinte rentabilidade (real):
Preço de venda na data da venda/preço de compra corrigido para a data da venda
= $11.000 / $10.000 x 1,20 = 0,9166 - 1 x 100 = - 8,33%
Em outras palavras, vendendo a $11.000,00 o aplicador recuperou somente 91,66% ($11.000,00/$12.000,00) do valor de seu investimento inicial quando consideramos o efeito da inflação. Logo, perdeu 8,33% de sua capacidade de compra (91,66% -1).
Outros exercícios sobre conversão de taxas
1) Um investidor aplicou $100.000,00 num título por 3 meses à taxa nominal de 6,5% a.t (ao trimestre). Sendo de 4,0% a inflação nesse período, calcular os rendimentos nominal e real auferidos pelo aplicador.
106.500 = 100.000 (1 + i)1
i = 6,5% no trimestre
i (mensal) = [(1 + 0,065)1/3 – 1] x 100 = 2,12% am (rentabilidade nominal por mês)
Perda pela Inflação do trimestre:
$ 100.000,00 x 4% = $ 4.000,00
Ganho Nominal = $ 6.500,00
Ganho Real = $ 2.500,00
r (trimestral) = $ 2.500,00/$ 100.000,00 x 1,04 = 2,4% a.t (rentabilidade real no trimestre)
r (mensal) = [(1 + 0,024)1/3 – 1] x 100 = 0,79% am (rentabilidade real por mês)
A taxa real pode ser obtida pelo emprego direto da fórmula:
r = [(1 + i)/(1 + I)] – 1 = [(1 + 0,065)/ (1 + 0,04)] – 1 = 2,4% at
2) Suponha que uma pessoa adquira, no início de determinado ano, um imóvel por $60.000,00, vendendo-o dois anos após por $85.320,00. Sendo de 31,1% a inflação no período determine a rentabilidade nominal e real anual desta negociação.
a) i (2 anos) = 85.320 = 60.000 (1 + i)1
i = 42,2% em dois anos
i (anual) = [(1 + 0,422)1/2 – 1] x 100 = 19,25%
b) r (2 anos) = [(1 + 0,42)/(1 + 0,31)] – 1 = 8,40% em dois anos
r (anual) = [(1 + 0,0847)1/2 – 1] x 100 = 4,15%
3) Determinar a variação real do poder aquisitivo de um assalariado que obtém em determinado semestre um reajuste salarial de 12%, admitindo que a inflação do período tenha atingido a: a) 8%; b) 12%; c) 20%.
a) r = (1,12/1,08) – 1 = 3,7%
b) r = (1,12/1,12) –1 = 0%
c) r = (1,12/1,20) –1 = - 6,67%
4) Sabe-se que o preço a vista de um imóvel é de $ 78.000,00. Na hipótese de serem oferecidos uma entrada de 40% e o saldo restante, corrigido pela inflação, pago após um semestre, determinar o valor deste pagamento, sabendo-se que a taxa de inflação projetada para um ano atinge 21%.
Valor a Financiar = $ 78.000,00 - 40% = $ 46.800,00
Taxa semestral de inflação = ((1,21)1/2 -1) x 100 = 10%.
Valor corrigido do pagamento
$ 46.800,00 x (1,1) = $ 51.480,00
5) A taxa nominal de juros contratada em um empréstimo é de 20% ao ano. Tendo ocorrido uma variação de 7% nos índices de preços neste mesmo período, determinar a taxa real anual de juros do empréstimo.
r = (1,2)/1,07) – 1 x 100 = 12,1495%
6) Uma aplicação de $ 38.600,00, pelo prazo de 7 meses, gera um resgate de $ 48.400,00. Sendo os juros reais de 1,5% a.m., calcular a taxa de inflação e a taxa nominal de juros desta operação.
FV = $ 48.400,00,
PV = $ 38.600,00
r = 1,5% a.m.
Correção monetária (I) = ?
i = ?
i (7 meses) =(48.400,00/38.600) - 1 = 25,39% ou 48.400 = 38.600 (1+i)1
i mensal = [(1 + 0,2539)1/7] - 1 = 3,29% am
I = [(1 + i)/(1 + r)] – 1 = (1,0329/1,015) - 1 = 1,76% am
7) Um banco negociou uma operação de capital de giro no valor de $ 1.000 pelo prazo de 60 dias. Sabendo-se que o juro foi de 80% ao ano, e que a empresa pagou uma comissão de 2% sobre o total na abertura do crédito. Qual a taxa interna de retorno (juro efetivo) da operação e a taxa real se a inflação foi de 4% no primeiro mês e de 5% no segundo mês?
PV = 1.000
i = 4% e 5%
Comissão (cc) = 2% Valor liberado = $980
i = 80% aa = 10,29% para 60 dias
IRR ?
ir ?
1102,9 = 980 (1 +i )
i = 1102,9/980 – 1
i = 12,54% para 60 dias
ir = (1+i)/[1 + I(1 + i)] - 1 = 1,125/1,092
ir = 3,058% para o período
8) Calcular o custo efetivo anual em moeda nacional de um empréstimo em moeda estrangeira contratado a juros nominais de 8%aa, com capitalização mensal, considerando uma desvalorização da moeda nacional de 2% am.
i efetiva mensal = 0,08/12 = 0,00667
i anual = (1,0067)12 x (1,02)12 = 1,08343 x 1,268 = 1,3737
i = 37,37% aa
9) Calcular o valor de resgate de uma operação pós-fixada com 3 meses de prazo, sabendo-se que o valor aplicado é de $ 1.000, a taxa de juro é de 2% ao mês e o índice de correção é de 15% no primeiro mês, 17% no segundo mês e 19% no terceiro.
FV = 1000 x (1,15) x (1,17) x (1,19) x (1,02)3
FV = $1.699,15
Assinar:
Postagens (Atom)
