Convenção e conversão de taxas

 Convenção e conversão de taxas

Algumas das taxas de juro utilizadas no mercado são definidas como ‘taxa de juro nominal’, como no caso do juro da poupança. Mas o que significa isso? Uma taxa nominal não é a que ganhamos, ou pagamos, efetivamente no fim do período, de um ano, por exemplo. Neste caso precisamos calcular, a partir da taxa nominal, a taxa efetiva embutida na operação. Ou seja, são muitas as convenções adotadas no mercado no que se refere a taxa de juros, e precisamos entender cada uma delas, do contrário não saberemos quanto pagamos por um empréstimo ou quanto recebemos por uma aplicação, além de nos impedir de converter essa taxa para períodos distintos.

.

TAXA NOMINAL E TAXA EFETIVA

Chama-se de taxa efetiva a taxa de juros que se obtém no processo de formação dos juros em regime composto, isto é, ao longo dos períodos de capitalização (geralmente ao longo dos meses). Quando é chamada de taxa nominal estamos tratando de uma definição matemática que considera que o intervalo de capitalização desse juro não é o mesmo daquele definido para a própria taxa. Por exemplo, suponhamos uma taxa nominal de juros de 12% ao ano. Caso não se diga mais nada esta taxa é considerada efetiva, ou seja, a taxa de juros é de 12% ao ano, capitalizada anualmente.

Mas, caso a taxa de juros venha acrescida de um período de capitalização diferente, como ‘12% ao ano,  capitalizada mensalmente’, vemos que os prazos não coincidem. Ou seja, o juro de 12% ao ano será capitalizado, incorporado ao principal, no fim de cada mês. Por isso a taxa é chamada de nominal. Neste caso, o prazo de capitalização (ou seja, período de formação e incorporação dos juros ao principal) é de um mês, e o prazo a que se refere a taxa de juros igual é de 1 ano (12 meses). O exemplo mais prático é o caso da poupança, definida em 6% de juro nominal ao ano. Todavia, como somos remunerados mensalmente na caderneta temos que dividir os 6% por 12 meses, o que nos dá 0,5% ao mês. Como temos juros sobre juros, isto é, todo mês a poupança rende 0,5% sobre o que já havia rendido no mês anterior, a taxa efetiva, no fim de 1 ano, acaba sendo de 6,168%; portanto, superior àqueles 6% da taxa nominal divulgada. Logo, temos as seguintes definições a partir deste exemplo da poupança:

.

* taxa nominal da operação para o período = 6% ao ano

* taxa proporcional simples (taxa definida para o período de capitalização) = 0,5% ao mês (6%/12 meses)

* taxa efetiva de juros anual (em juro composto) = 6,168% ao ano



CONVERSÃO DE TAXAS: TAXAS PROPORCIONAIS E EQUIVALENTES 

Surge um problema ao se converter taxas para períodos distintos. Taxas proporcionais são calculadas em juro simples, precisando neste caso apenas de uma regra de três.  Porém, quando falamos em conversão de taxas, geralmente estamos tratando de taxas equivalentes, isto é, em juro composto. Logo,

.

TAXAS PROPORCIONAIS

Qual a taxa mensal proporcional (juros simples) a uma taxa de 6% ao trimestre?

Por regra de três achamos a taxa mensal

6%  ____ 3 meses (= 1 trimestre)

x ?  ____  1 mês

x = 2% ao mês



TAXAS EQUIVALENTES

Com o nosso interesse maior aqui é o juro composto, temos a seguinte fórmula para conversão de taxas equivalentes (a juros compostos):

onde,

i_n = taxa que procuramos

i_x = taxa dada

n = dias (ou meses) contidos na taxa procurada

x = dias (ou meses) contidos na taxa dada

Exemplos

1) Qual a taxa mensal proporcional (juros simples) a uma taxa de 6% ao trimestre?

i_n = mensal (1 mês ou 30 dias)

i = trimestre (3 meses ou 90 dias)

n = 1 meses (ou 30 dias)

x = 1 trimestre (ou 90 dias)

Podemos resolver essa conversão trabalhando com dias ou meses, desde que mantenhamos a compatibilidade ao lançarmos isso na fórmula (mês com mês ou dias com dias).

i_{30 (dias)} = [(1 + 0,06)^{30/90 (dias)} –1] x 100

i₃₀ = [(1,06) ^0,3333 –1] x 100

i₃₀ = 1,961%


Ou


i_1(mês)= [(1 + 0,35)^{1/3 (meses)} –1] x 100

i₁ = [(1,06) ^0,3333 –1] x 100

i₁ = 1,961%



(f) (REG) 1,06 (ENTER) 30 (ENTER) 90 (÷) (Y^x) 1 (-) 100 (x)

i = 1,961%

(f) (REG) 1,06 (ENTER) 1 (ENTER) 3 (÷) (Y^x) 1 (-) 100 (x)

i = 1,961%



2) Qual a taxa bimestral equivalente à taxa semestral de 35%?

i_n = bimestral

i = semestral

n = 60

x = 180

i₆₀ = [(1 + 0,35)^60/180 –1] x 100

i₆₀ = [(1,35) ^0,3333 –1] x 100

i₆₀ = 10,52%



(f) (REG) 1,35 (ENTER) 60 (ENTER) 180 (÷) (Y^x) 1 (-) 100 (x)

i = 10,52%


3) Qual a taxa semestral equivalente à taxa trimestral de 5%?

i₁₈₀ = [(1 + 0,05)^180/90 –1] x 100

i₁₈₀ = [(1,05) ² –1] x 100

i₁₈₀ = 10,25%


(f) (REG) 1,05 (ENTER) 180 (ENTER) 90 (÷) (Y^x) 1 (-) 100 (x)

i = 10,25%


4) Qual a taxa diária equivalente à taxa trimestral de 90%?

i₁ = [(1 + 0,90)^1/90 –1] x 100

i₁₈₀ = [(1,90) ^0,0111 –1] x 100

i₁₈₀ = 0,7157%


(f) (REG) 1,90 (ENTER) 1 (ENTER) 90 (÷) (Y^x) 1 (-) 100 (x)

i = 0,7157%



TAXA NOMINAL (APARENTE) E TAXA REAL

    Inflação acumulada

Já vimos em outra lição como considerar o efeito da taxa de inflação ao longo do tempo. Inflação acumulada, que não pode se resumir à soma das inflações. Aprofundemos um pouco esse estudo.

A inflação se processa de maneira exponencial, sendo acrescida sobre a inflação do período anterior, ou seja, o aumento de preço ocorre sobre um valor que já incorpora acréscimos apurados anteriormente. Como nos juros compostos, temos inflação sobre inflação.

Suponhamos que um bem no valor de $ 1.000,00 seja reajustado mensalmente pela inflação, sendo ela de 2,8%, 1,4% e 3,0%, em períodos consecutivos.

1º mês: $ 1.000,00 x (1.028)¹  = $ 1.028,00

2º mês: $ 1.028,00 x (1,014)¹ = $ 1.042,39

3º mês: $ 1.042,39 x (1,03)¹ = $ 1.073,66

O incremento do valor do ativo no trimestre é de 7,366% ($ 1.073,66,/ $ 1.000,00), o que equivale ao produto (capitalização composta) das taxas mensais de inflação, isto é:

.

Inflação do Trimestre = [[(1,028) x (1,014) x (1,03)] –1] x 100 = 7,366%

.

* as taxas, quando multiplicadas, dever ser somadas a 1 (link para cálculo da inflação acumulada, por diversos índices, a partir de 2000: http://fundos.economia.uol.com.br/uol/calculadora-indices-inflacao/)

.

A taxa equivalente mensal de inflação do período, identicamente ao regime de juros compostos, é:

Taxa Equivalente Mensal = [(1 + 0,0737)^1/3 – 1] x 100 = 2,398% ao mês

 * observem que essa taxa equivalente mensal de 2,398% é como uma média das inflações dos 3 meses (2,8%, 1,4% e 3%), pois os resultados são praticamente idênticos, já que (2,8 + 1,4 + 3)/3 = 2,4%. Por isso chamamos a taxa equivalente de taxa média.

.

Se o trimestre apresentasse uma deflação no terceiro mês teríamos: 2,8%, 1,4% e - 3% (deflação). A taxa de inflação acumulada do período seria:

Inflação do Trimestre = [[(1 + 0,028) x (1 + 0,014) x (1 – 0,03)] –1] x 100  = 1,11%



Exemplos

1) A taxa mensal de inflação de um quadrimestre (4 meses) atinge, respectivamente: 2,8%, 3,4%, 5,7% e 8,8%. Determinar a taxa de inflação acumulada do período e a taxa média mensal.

(f) (REG) 1,028 (ENTER) 1,034 (x) 1,057 (x) 1,088 (x)

I = 22,2% ao quadrimestre

(f) (REG) 1,222 (ENTER) 4 (1/x) (Y^x) 1 (-) 100 (x)

I= 5,15% ao mês

2) A taxa de inflação da economia de determinado ano foi de 748.95%.  Calcu­lar a taxa equivalente semestral inflação do período.

(f) (REG) 1 (ENTER) 7,4895 (+) 2 (1/x) (Y^x) 1 (-) 100 (x)

I = 191,4% ao semestre

3) Sendo projetada em 1,9% ao mês a taxa de inflação para os próximos 5 meses, determinar a inflação acumulada deste período.

(f) (REG) l,0l9 (ENTER) 5 (Y^x) 1 (-) 100 (x)

I = 9,87%  p/ 5 meses

4) Determinado trimestre apresenta as seguintes taxas mensais de variações nos preços gerais da economia: 7,2%, 2,9% e - 1,2% (deflação). Determinar a taxa de inflação acumulada do trimestre.

Como temos uma taxa negativa lembremos que:

[(1 + 0,072) x (1 + 0,029) x (1- 0,012)] - 1 = 8,99% a.t.

(f) (REG) 1,072 (ENTER) 1,029 (x) 0,988 (x) 1 (-) 100 (x)

I = 8,99% a.t.



Taxa aparente e taxa real

Já vimos acima que a taxa de juros nominal (linear) indica a descapitalização do juro de forma proporcional (juros simples). No caso da poupança a taxa nominal é de 6%. Todavia o conceito de taxa de juro nominal também pode ter outro significado, neste caso quando a comparamos com a inflação, podendo ser chamada de nominal ou aparente. Lá mostramos a diferença entre taxa nominal e taxa efetiva, pois interessava o regime de capitalização dessa taxa nominal para descobrirmos a efetiva. Como aqui o que importa é o efeito da inflação, separamos a taxa nominal (ou aparente) da inflação e encontramos a taxa real.

O termo real para as operações de Matemática Financeira denota um resultado apurado livre dos efeitos inflacionários. Ou seja, quanto se ganhou (ou perdeu) verdadeiramente, sem a interferência das variações verifica­das nos preços. O objetivo do cálculo da taxa real (r) é o de expurgar a indexação da taxa total de juros (nominal), de maneira a expressar o juro real.

A fórmula de apuração da taxa real é a seguinte:



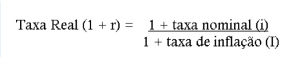
Logo,





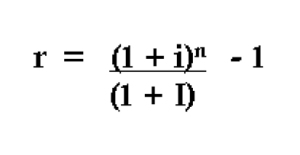
onde:

i = rentabilidade nominal (ou aparente)

I = inflação

r = rentabilidade real

Substituindo-se os valores da inflação e ganho nominal (taxa nominal) do exemplo acima tem-se:

r =  [(1 + 0,10) / (1 + 0,20)] - 1  =  1,10  -1  =   - 8,33% ($1.000/$12.000)

 * A taxa real também pode ser negativa, desde que a inflação supere a varia­ção nominal dos juros.

Comprovação da fórmula:

A inflação tende a corroer o poder de compra da moeda. Suponhamos que uma pessoa tenha adquirido um imóvel por $ 10.000,00 em certa data, e vendido, um ano depois, por $11.000,00. Consideremos ainda uma inflação de 20% no período. É comum diminuir o preço de venda do preço de compra para se determinar o ganho, que neste caso é apenas nominal (ou aparente). Para saber o ganho real, temos que retirar o efeito da inflação no período.

No exemplo, tem-se um lucro nominal (aparente) de $1.000. Observe que para não ocorrer prejuízo, o imóvel deveria ser vendido por um preço 20% maior que o seu valor de compra há um ano, ou seja, por $12.000 (10.000 + 20% de inflação). Somente a partir desse valor é que efetivamente existiria um lucro real. Portanto, a venda por $11.000 mostra um prejuízo real de $1.000,00, pois caso retiremos o preço de venda (11.000) do preço corrigido ($12.000), percebemos o rendimento perdeu para a inflação.

Em termos de rentabilidade notamos que o ganho nominal, como já visto, seria:

Ganho Nominal =    $1.000,00/$10.000   x 100 = 10%

Quando consideramos a inflação temos a seguinte rentabilidade (real):



Preço de venda na data da venda/preço de compra corrigido para a data da venda

= $11.000 / $10.000 x 1,20 = 0,9166  - 1 x 100  = - 8,33%

 Em outras palavras, vendendo a $11.000,00 o aplicador recuperou somente 91,66% ($11.000,00/$12.000,00) do valor de seu investimento inicial quando consideramos o efeito da inflação. Logo, perdeu 8,33% de sua capacidade de compra (91,66% -1).

Outros exercícios sobre conversão de taxas

1) Um investidor aplicou $100.000,00 num título por 3 meses à taxa nominal de 6,5% a.t (ao trimestre). Sendo de 4,0% a inflação nesse período, calcular os rendimen­tos nominal e real auferidos pelo aplicador.

106.500 = 100.000 (1 + i)¹

i = 6,5% no trimestre

i (mensal) = [(1 + 0,065)^1/3 – 1] x 100 = 2,12% am (rentabilidade nominal por mês)

Perda pela Inflação do trimestre:

$ 100.000,00 x 4%  = $ 4.000,00

Ganho Nominal = $ 6.500,00

Ganho Real = $ 2.500,00

r (trimestral) = $ 2.500,00/$ 100.000,00 x 1,04 =  2,4% a.t (rentabilidade real no trimestre)

r (mensal) = [(1 + 0,024)^1/3 – 1] x 100 = 0,79% am (rentabilidade real por mês)

A taxa real pode ser obtida pelo emprego direto da fórmula:

r = [(1 + i)/(1 + I)] – 1 =  [(1 + 0,065)/ (1 + 0,04)] – 1 = 2,4% at

2) Suponha que uma pessoa adquira, no início de determinado ano, um imóvel por $60.000,00, vendendo-o dois anos após por $85.320,00. Sendo de 31,1% a inflação no período determine a rentabilidade nominal e real anual desta negociação.

a) i (2 anos) =  85.320 = 60.000 (1 + i)¹

i = 42,2% em dois anos

i (anual) = [(1 + 0,422)^1/2 – 1] x 100 = 19,25% 



b) r (2 anos) = [(1 + 0,42)/(1 + 0,31)] – 1 = 8,40% em dois anos

r (anual) = [(1 + 0,0847)^1/2 – 1] x 100 = 4,15%

3) Determinar a variação real do poder aquisitivo de um assalariado que obtém em determinado semestre um reajuste salarial de 12%, admitindo que a inflação do período tenha atingido a: a) 8%; b) 12%; c) 20%.

a) r  = (1,12/1,08) – 1 = 3,7%

b)  r  = (1,12/1,12) –1 = 0%

c) r = (1,12/1,20) –1 =  - 6,67%

4) Sabe-se que o preço a vista de um imóvel é de $ 78.000,00. Na hipótese de serem oferecidos uma entrada de 40% e o saldo restante, corrigido pela inflação, pago após um semestre, determinar o valor deste pagamento, sabendo-se que a taxa de inflação projetada para um ano atinge 21%.

Valor a Financiar = $ 78.000,00 - 40% =  $ 46.800,00

Taxa semestral de inflação = ((1,21)^1/2  -1) x 100 = 10%.

Valor corrigido do pagamento

$ 46.800,00 x (1,1) = $ 51.480,00

5) A taxa nominal de juros contratada em um empréstimo é de 20% ao ano. Tendo ocorrido uma variação de 7% nos índices de preços neste mesmo período, determinar a taxa real anual de juros do empréstimo.

r = (1,2)/1,07) – 1 x 100 = 12,1495%

6) Uma aplicação de $ 38.600,00, pelo prazo de 7 meses, gera um resgate de $ 48.400,00. Sendo os juros reais de 1,5% a.m., calcular a taxa de inflação e a taxa nominal de juros desta operação.

FV = $ 48.400,00,

PV = $ 38.600,00

r = 1,5% a.m.

Correção monetária (I) = ?

i = ?

i (7 meses) =(48.400,00/38.600) - 1 = 25,39%  ou  48.400 = 38.600 (1+i)¹ 

i mensal = [(1 + 0,2539)^1/7] - 1 = 3,29% am



I = [(1 + i)/(1 + r)]  – 1 =  (1,0329/1,015) - 1 = 1,76% am

7) Um banco negociou uma operação de capital de giro no valor de $ 1.000 pelo prazo de 60 dias. Sabendo-se que o juro foi de 80% ao ano, e que a empresa pagou uma comissão de 2% sobre o total na abertura do crédito. Qual a taxa interna de retorno (juro efetivo) da operação e a taxa real se a inflação foi de 4% no primeiro mês e de 5% no segundo mês?

PV = 1.000

i = 4% e 5%

Comissão (cc) = 2%  Valor liberado = $980

i = 80% aa = 10,29% para 60 dias

IRR ?

ir ?

1102,9 = 980 (1 +i )

i = 1102,9/980 – 1

i = 12,54% para 60 dias

ir = (1+i)/[1 + I(1 + i)] - 1 =  1,125/1,092

ir = 3,058% para o período

8) Calcular o custo efetivo anual em moeda nacional de um empréstimo em moeda estrangeira contratado a juros nominais de 8%aa, com capitalização mensal, considerando uma desvalorização da moeda nacional de 2% am.

i efetiva mensal = 0,08/12 = 0,00667

i anual = (1,0067)¹² x (1,02)¹² = 1,08343 x 1,268 = 1,3737

i = 37,37% aa

9) Calcular o valor de resgate de uma operação pós-fixada com 3 meses de prazo, sabendo-se que o valor aplicado é de $ 1.000, a taxa de juro é de 2% ao mês e o índice de correção é de 15% no primeiro mês, 17% no segundo mês e 19% no terceiro.

FV = 1000 x (1,15) x (1,17) x (1,19) x (1,02)³

FV = $1.699,15